1613. Два числа и четыре действия

Над двумя целыми положительными числами были выполнены следующие четыре действия:

· их сложили;

· вычли из большего меньшее;

· перемножили;

· разделили большее на меньшее.

После сложения всех результатов получили число n. Найдите все пары таких чисел.

Вход. Одно натуральное число n (1 ≤ n ≤ 10¹²).

Выход. В отдельных строках выведите по одной паре чисел (x, y), x ≤ y, удовлетворяющих условию задачи. Пары должны быть упорядочены по возрастанию x. Если нет ни одной пары чисел, удовлетворяющей условию, выведите “NO SOLUTION” (без кавычек).

Пример входа 1	Пример выхода 1
4	1 1
Пример входа 2	Пример выхода 2
1	NO SOLUTION
Пример входа 3	Пример выхода 3
243	2 54 8 24

РЕШЕНИЕ

перебор

Анализ алгоритма

Пусть x, y (x ≤ y) – входные числа. В результате четырех действий получим следующие результаты:

· x + y : их сложили;

· y – x : вычли из большего меньшее;

· x * y : перемножили;

· y / x : разделили большее на меньшее.

Просуммируем четыре полученных числа:

2y + x * y + y / x = = = n

Переберем значение x от 1 до . Если n делится на (x + 1)², то получим пару, в которой

y =

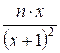
Реализация алгоритма

Читаем значение n.

scanf("%lld", &n);

Если станет flag = 1, то хотя бы одна пара (x, y) будет найдена.

flag = 0;

for (x = 1; x * x <= n; x++)

{

if (n % ((x + 1) * (x + 1)) == 0)

{

flag = 1;

y = n / ((x + 1) * (x + 1)) * x;

printf("%lld %lld\n", x, y);

}

}

Если ни одна пара (x, y) не найдена, выводим “NO SOLUTION”.

if (!flag) puts("NO SOLUTION");